«Цифры врут»: как читать числа и не попасть в «ловушки статистики»

В 2013 г. Флойд Норрис, финансовый корреспондент The New York Times, опубликовал колонку, посвященную изменениям медианной заработной платы в США за 2000–2013 гг. Данные о динамике зарплаты выглядели парадоксально: по всей стране медианная зарплата в реальном выражении выросла примерно на 1%, однако если полную выборку разделить на подгруппы по уровню образования работников, то в каждой из подгрупп медианная зарплата за тот же период снизилась. Каким образом, если все части выборки показывают снижение, сама выборка в целом показывает рост? Некоторые читатели решили, что автор колонки просто ошибся.

Однако это не так: эта «статистическая аберрация» возникла потому, что относительный размер образовательных групп в выборке сильно изменился за 13 лет, пояснил через несколько дней после выхода колонки в своем блоге Норрис. Количественная доля выпускников колледжей выросла, тогда как доля закончивших только среднюю школу снизилась, следовательно, в целом лучше образованных (а значит, имеющих более высокий заработок) людей стало больше, что повысило медианную зарплату по всей выборке.

Описанный статистический эффект – когда тренд, проявляющийся в агрегированной выборке, противоречит трендам в составных частях этой выборки – называется парадоксом Симпсона, по имени британского статистика Эдварда Симпсона, описавшего это явление в 1951 г. Этот парадокс встречается повсеместно, от квантовой механики и оценки гендерного неравенства среди абитуриентов до результатов образовательных тестов и расчета процента выживших после крушения «Титаника».

С описания парадокса Симпсона начинается книга экономиста Дэвида Чиверса и научного журналиста Тома Чиверса «Цифры врут. Как не дать статистике обмануть себя», которая вышла в переводе на русский язык в августе 2022 г. в издательстве Individuum. Вот так авторы поясняют этот парадокс на условном примере с заработками с помощью таблички:

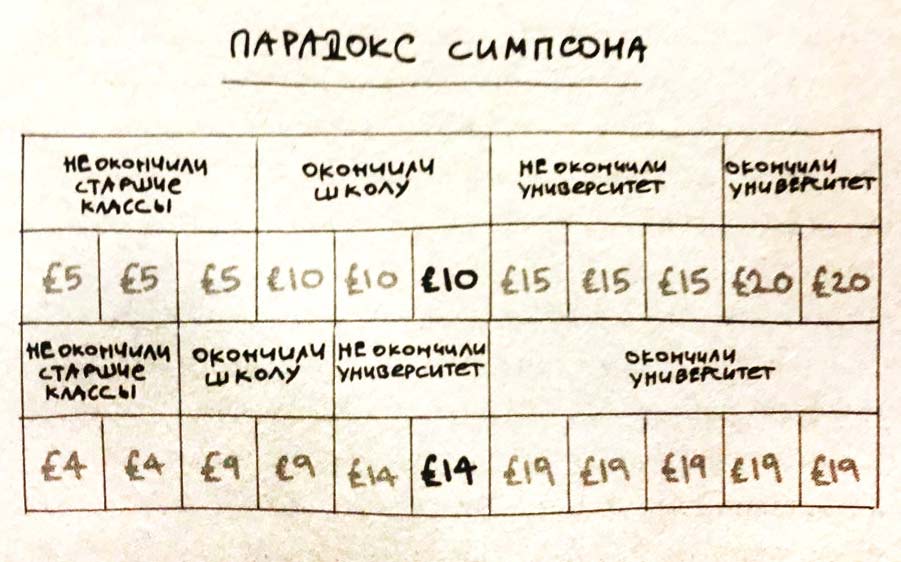
Как видно из таблицы, заработок сократился во всех четырех подгруппах выборки: у не окончивших школу – с 5 до 4 фунтов, у окончивших школу – с 10 до 9, у не окончивших университет – с 15 до 14, окончившие университет стали зарабатывать 19 фунтов вместо 20. Но за счет того, что доля подгруппы окончивших университет, имеющей самый высокий заработок, выросла при снижении доли других групп, медианный заработок всей выборки вырос с 10 до 14 фунтов.

Парадокс Симпсона свидетельствует, насколько важно соблюдать осторожность и аккуратность при работе с данными и как легко – сознательно или неумышленно – впасть в заблуждение при их интерпретации и подаче. «Числами легко затуманить смысл и сбить с толку, и многие (в особенности политики, но не они одни) пользуются этим. <…> Чтобы ориентироваться во всем этом, необязательно быть математиком, но нужно понимать, как числа подсчитываются, для чего применяются и какие с ними бывают подвохи. Иначе мы – как отдельные индивидуумы и как общество в целом – будем принимать неверные решения», – пишут авторы книги.

Авторы проанализировали, как обычные с виду числа «могут удивительным образом сбивать с толку», описав основные «ловушки статистики» и ошибки, которые могут возникать при интерпретации и подаче данных.

Книга разделена на 22 главы, в каждой из которых рассмотрен какой-то один способ неправильной интерпретации данных. Все объяснения составлены так, чтобы быть понятными читателю, не владеющему математическими методами, но для желающих разобраться подробнее в главах есть специальные врезки с математическими объяснениями.

Смещенная выборка и «ошибка выжившего»

Одна из самых очевидных причин, по которым результаты исследования могут оказаться недостоверными, – используемая выборка оказывается смещенной, или предвзятой. Например, если попытаться вычислить средний рост населения, измеряя случайных прохожих на съезде баскетболистов, очевидно, что средний рост в выборке резко подскочит, хотя для населения в целом останется неизменным. Вред от смещенных выборок отличается от вреда маленьких выборок (также способствующих неточным результатам исследований): при выборе небольших групп случайным образом увеличение размера выборки позволит приблизиться к получению более точного результата, тогда как при изучении смещенной выборки будет расти лишь уверенность исследователя в результате, в действительности ошибочном.

Один из типов смещения выборки приводит к статистическому искажению под названием «ошибка выжившего» (survivorship bias) – в этом случае человек делает заключения, основываясь только на известных данных («выживших»), и не учитывает неизвестные, но все же существующие сведения («погибшие»).

Во время Второй мировой войны представительная группа экономистов и статистиков проводила исследования для военно-морских сил США – в эту группу входили, например, Милтон Фридман и Джордж Стиглер, будущие лауреаты Нобелевской премии по экономике. Одна из задач, которые решали в то время военные, касалась укрепления американских бомбардировщиков броней. При этом вес брони снижал скорость, маневренность и дальность полета, поэтому покрывать ею весь самолет не стоило, и предстояло определить, укрепление каких частей было бы наиболее эффективно. Изучив повреждения самолетов, вернувшихся с боевых заданий, авиаконструкторы пришли к выводу, что броню следует установить на крыльях и фюзеляже, поскольку именно там чаще всего обнаруживались повреждения и пробоины от снарядов и пуль. Однако входивший в группу статистиков Абрахам Вальд указал на ошибочность этого подхода – ведь конструкторы учитывали только «выжившие» самолеты, то есть, сами того не понимая, изучали смещенную выборку. Вальд предположил, что попадания в бою были равномерно распределены по разным частям самолетов, из чего следовало, что самолеты, получившие попадания в более уязвимые части, например в топливную систему или двигатель, с меньшей вероятностью возвращались на базу. Таким образом, укреплять броней следовало, наоборот, те места, повреждения которых у вернувшихся самолетов были наименьшими.

«Ошибка выжившего» может проявляться и в самых обыденных жизненных ситуациях. Один из примеров – книги успешных предпринимателей на тему «секреты моего успеха». Всем хочется узнать, как заработать миллионы, поэтому такие книги идут нарасхват, но чаще всего они представляют собой список ошибок выжившего.

Кроме того, «ошибка выжившего» – пример более широкой проблемы: проблемы выбора по зависимой переменной. «Идея проста: вы не можете понять, почему происходит Х, рассматривая только те случаи, когда Х происходит», – поясняют Дэвид и Том Чиверсы. В научном эксперименте независимая переменная – это то, что экспериментатор может менять (например, доза лекарства), а зависимая переменная – это то, что экспериментатор измеряет, чтобы проверить, изменилась она или нет (например, доля излечившихся).

Представьте, что вы решили выяснить, ведет ли потребление воды (независимая переменная) к артриту (зависимая переменная), приводят пример авторы. Пересмотрев всех больных артритом, вы быстро убедитесь, что все они пили воду. Но поскольку в выборке нет тех, кто не болеет артритом, то неизвестно, пьют ли больные артритом больше воды, чем все остальные.

Казалось бы, это настолько очевидная ошибка, что зачем о ней и говорить, – однако подобные ошибки происходят сплошь и рядом. «Как только происходит массовая стрельба, СМИ смотрят на биографию стрелка и находят, что тот играл в жестокие видеоигры. <…> Это столь же очевидный пример выбора по зависимой переменной, как и в случае с водой и артритом», – пишут авторы. Вопрос не в том, играют ли организаторы массовой стрельбы в жестокие видеоигры, а в том, играют ли они в эти игры больше других людей. А еще надо посмотреть на направление причинно-следственной связи: становятся ли люди жестокими, потому что играют в жестокие видеоигры, или же играют в такие игры, потому что жестоки. Более того, минимум одно исследование показало, что распространение таких игр приводит к снижению насилия – возможно, потому, что люди, которые могли бы выйти из дома и выплеснуть агрессию, остаются у себя в комнате и играют в видеоигру. «Сообщения, что массовый убийца играл в жестокую видеоигру, удивляют немногим больше, чем утверждение, что он ел пиццу или носил футболку», – сравнивают авторы.

Искажающие факторы и «ошибка коллайдера»

Одна из самых распространенных ошибок в исследованиях и оценках – путаница между корреляцией и причинно-следственной связью. Один из примеров, которыми часто иллюстрируют разницу между этими двумя понятиями, – мороженое и утопленники: в дни, когда продажи мороженого растут, увеличивается количество утонувших людей. Однако если учесть температуру воздуха (в жаркий день люди с большей вероятностью покупают мороженое, отчего растут продажи; и чаще купаются, что повышает риск утонуть), связь между продажами мороженого и числом утопленников пропадает. Температура в этом примере – искажающий фактор, который влияет на обе переменные.

Представьте, что вы решили выяснить, с какой скоростью бегают люди, и обнаружили интересный феномен, предлагают авторы: чем больше у человека седых волос – тем медленнее он пробегает милю. Возможно, седина замедляет бег. Но, скорее всего, есть некий третий фактор, с которым, как и в примере с мороженым, связаны обе переменные: возраст. Видимо, чем человек старше, тем больше у него седых волос, и чем он старше – тем медленнее бегает. Если не учитывать (экономисты говорят – контролировать) искажающие переменные, могут получиться результаты вроде выдуманной связи, что седые волосы ведут к замедлению скорости бега.

Более «жизненный» пример: обнаруженная корреляция между выбросами углекислого газа и ожирением. Следует ли из этого, что углекислый газ делает людей толстыми? Скорее всего, дело в том, что мир богатеет, а становясь богаче, люди тратят больше на высококалорийную пищу и на товары и услуги, связанные с выделением углекислого газа (например, на автомобили и электричество). Если это учесть, станет понятно, что никакой связи между ожирением и выбросами СО2, скорее всего, нет, однако важную роль и в том и в другом играет третья переменная – ВВП. «Если в новостях пишут, что Х связано с Y, не стоит думать, что из этого непременно следует, что Х влечет за собой Y или наоборот. Возможно, есть еще скрытое Z, которое вызывает и Х, и Y», – советуют авторы.

Контроль искажающих факторов очень важен и входит в кодекс чести статистиков. Однако это не значит, что нужно учитывать как можно больше переменных, предполагая, что все они искажающие: это не всегда верно. Более того, иногда после добавления в анализ дополнительного фактора две переменные покажутся связанными, хотя на деле это не так. В этом случае может возникнуть статистическая аномалия под названием «ошибка коллайдера» (collider bias): исследователь полагает, что контролирует искажающую переменную, чтобы устранить смещение, а на самом деле вводит переменную-коллайдер и, наоборот, тем самым случайно создает смещение.

Коллайдер – это противоположность искажающего фактора: если искажающий фактор является причиной для коррелирующих между собой переменных (например, возраст влияет и на количество седых волос, и на скорость бега), то в случае с коллайдером – наоборот, коррелирующие переменные оказывают влияние на него, то есть являются причиной переменной-коллайдера («коллайдером» такой фактор называется из-за того, что в графических моделях причинных связей стрелочки, ведущие к нему от переменных, сталкиваются).

Одна из сфер, в которой проявляется «ошибка коллайдера», – здравоохранение: именно эта ошибка может искажать понимание риска и тяжести заболевания коронавирусом, отмечали в своем исследовании эпидемиологи из Бристольского университета. Например, в начале пандемии выяснилось, что среди госпитализированных с ковидом доля курильщиков была меньше, чем среди населения в целом. Это было удивительно: курение негативно влияет на респираторную систему, которую как раз поражает коронавирус. В СМИ даже появились обсуждения, что курение может защищать от коронавируса, а аптекам пришлось ограничивать продажу никотиновых пластырей, на которые вспыхнул спрос. Однако попадавшие в больницы не всегда отражали состав населения в целом, поскольку отбирались по вполне определенным причинам. На раннем этапе пандемии тестировали не случайных людей: часто это были медицинские работники – а они курят меньше, чем население в целом; вторая группа, включавшаяся в число тестируемых, – люди с серьезными симптомами заболевания. При положительном тесте и тех и других госпитализировали, поэтому среди получивших положительный результат теста на ковид был выявлен большой процент некурящих медицинских работников.

Закон Гудхарта

Многие из рассмотренных в книге Дэвида и Тома Чиверсов статистических искажений могут иметь важные социально-экономические последствия. К таким искажениям относится и закон Гудхарта – названный по имени советника председателя Банка Англии Чарльза Гудхарта, заметившего, что «любая наблюдаемая статистическая закономерность склонна к разрушению, как только на нее оказывается давление с целью контроля». Этот закон чаще цитируют так: «Как только индикатор становится целью – он перестает быть хорошим индикатором».

Чтобы понять, как это работает, авторы приводят условный пример из сферы образования (закон Гудхарта часто проявляется именно в социально-экономических сферах): представим, что ученики из одних школ достигают в жизни более высоких успехов, чем из других, – чаще поступают в университеты, находят более высокооплачиваемую работу и вообще процветают и становятся высокообразованными гражданами. Проведенный анализ показал, что такие люди получали в школе более высокие оценки. Можно прийти к выводу, что вот он, прекрасный показатель, по которому можно ранжировать работу школ. И стартует реформа: школы с более высокой долей отличников начинают награждаться, с низкой – получать различные «штрафные санкции». Вскоре окажется, что доля отличников везде резко возросла. Но еще окажется, что выпускники школ, несмотря на свои блестящие аттестаты, не кажутся такими уж высокообразованными гражданами, как представлялось при запуске реформы.

Нетрудно догадаться, что произошло, рассуждают авторы: директора школ и органы управления образованием надавили на учителей, требуя увеличения доли высоких оценок. И хотя педагоги, несомненно, искренне пытались подтянуть отстающих, им быстро стало очевидно, что невыполнение целевых показателей плохо скажется на их карьере. Тогда некоторые учителя постарались найти самый быстрый и простой способ достижения необходимых показателей. А самый быстрый и простой способ – обмануть систему. Не всесторонне развивать учеников, поощряя любознательность и опираясь на сильные стороны каждого, а дать ученикам сотни примеров из экзаменов прошлых лет и «натаскать» на правильные ответы.

Это гипотетический пример, оговаривают авторы, но что-то похожее случается и в реальной жизни. По закону Гудхарта развивалась и ситуация со всемирно известным рейтингом Doing Business Группы Всемирного банка. Как только продвижение в этом рейтинге ряд правительств поставили себе в качестве политических целей, это привело, с одной стороны, к чисто «механической» правке законов ради лучшего соответствия критериям рейтинга без стремлений реально улучшить ситуацию, с другой – к попыткам повлиять на данные рейтинга. В итоге в 2021 г. составление рейтинга было прекращено.

Задача обойти закон Гудхарта остро стоит на всех уровнях управления как государством, так и компаниями, пишут Дэвид и Том Чиверсы. Для этого, например, можно использовать в качестве целевого не один показатель, а несколько и часто менять их. Однако никакие измерения не охватят реальность полностью – она всегда сложнее, рассуждают авторы: поиск идеальной статистической характеристики сродни стремлению «поместить на обложку книги такой крутой отзыв, что читать саму книгу уже не понадобится».