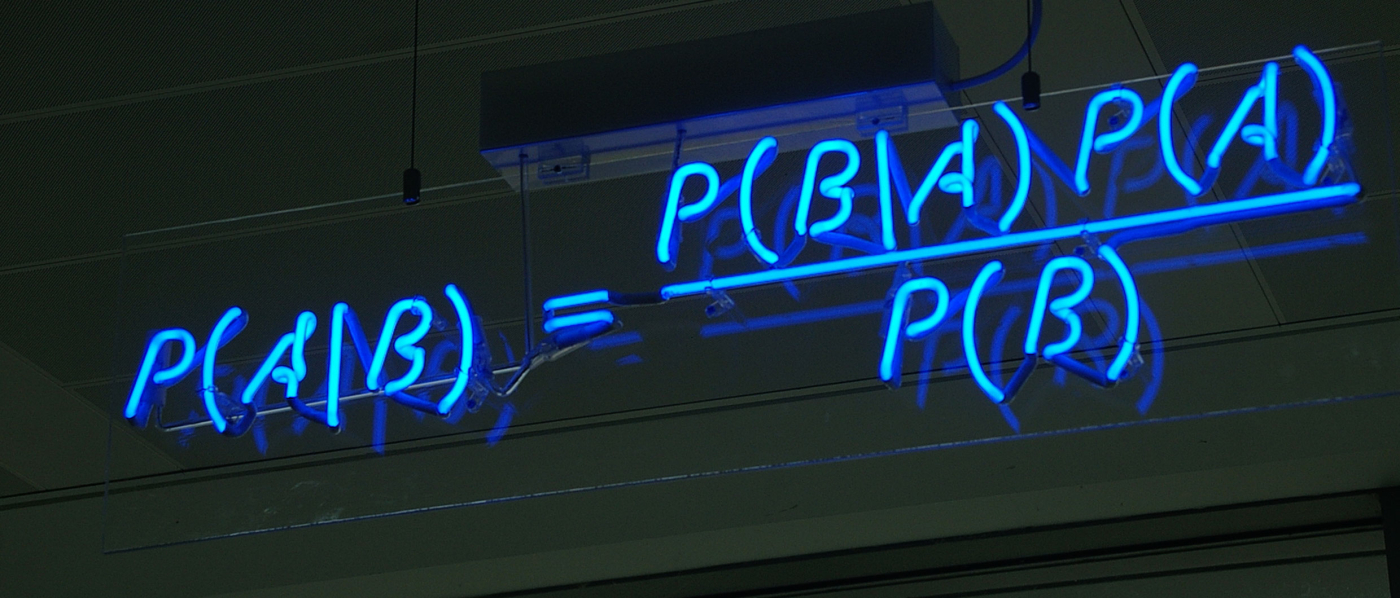«Формула всего»: универсальная теорема Байеса для объяснения реальности
Все люди непрерывно предсказывают будущее. Звучит странно. Но в действительности, принимая решение, например, во сколько утром выйти из дома, мы прогнозируем, сколько времени понадобится, чтобы добраться на работу к определенному часу; отправляемся в магазин за углом, чтобы купить там любимый сорт печенья; в разговоре с другом избегаем упоминаний о его недавнем разводе, прогнозируя, что ему это будет неприятно; и даже просто с каждым вдохом безотчетно делаем прогноз, что этим воздухом можно дышать. Так устроено человеческое сознание: его прогностичность позволяет не просто принимать некие важные решения, она обеспечивает саму возможность взаимодействовать с окружающим миром и существовать в нем, не спотыкаясь на каждом шагу при ходьбе.
Разумеется, приходится делать и намного более сложные прогнозы. Экономисты в центральных банках прогнозируют динамику инфляции, чтобы решить, повышать или понижать ставку. Эпидемиологи рассчитывают пик сезонной заболеваемости, чтобы спрогнозировать нагрузку на больницы. Метеорологи строят прогноз погоды, чтобы предупредить о шторме или засухе.
Все прогнозы, от простейших до самых сложных, объединяет одно: они требуют периодического уточнения – потому что ситуация периодически же меняется.
Все люди – прогностические машины, а Томас Байес показал, как это работает математически, рассказывает научный журналист Том Чиверс в новой книге «Предсказать все»: «Жизнь – не шахматы, в ней нет полной информации, и поэтому ее нельзя «решить», как какую-то задачу. Она больше похожа на покер: игру, в которой человек пытается принимать оптимальные решения, обладая небольшим объемом данных. Эта книга – об уравнении, которое позволяет это делать».
Уравнение, о котором идет речь, – это теорема (также формула) Байеса:
P(А|В) = P(B|A) * P(A) / P(B)
P – это вероятность, вертикальная черта | – это сокращенное обозначение «в случае, если» или «при условии, что», то есть P(А|В) – вероятность события А при условии события B.
В самом общем виде смысл теоремы Байеса сводится к утверждению, что изначальное (априорное) суждение (событие А), дополненное новой информацией (событие В), даст более приближенную к реальности картину. Другими словами, логика Байеса дает возможность уточнить вероятность того или иного события, учитывая и ранее известные факты, и новые наблюдения.
Полностью формула читается так: вероятность (P) события A с учетом события B равна вероятности B с учетом A, умноженной на вероятность A саму по себе и деленной на вероятность B саму по себе.
Выглядит запутанно, поэтому поясним на простом примере. Допустим, дорога из дома до работы занимает час (событие А, априорная информация), но накануне ночью был сильный снегопад, засыпавший дороги (событие В, новые данные), – какова вероятность доехать до работы за час сегодня?
P(A) – это обычная вероятность доехать до работы за час. Например, в среднем это удавалось почти всегда, в 9 случаях из 10: P(A) = 0,9.
P(B) – это обычная вероятность события В: насколько часто вообще бывает снег? К примеру, в Москве осадки в виде снега бывают в среднем примерно 70 дней в году: P(B) = 70/365 = 0,2 (или 48/250 = 0,2, при допущении, что снег идет равномерно и в нерабочие дни, и в рабочие, которых около 250, или примерно две трети).
P(B|A) – а это ключевой «ингредиент» формулы Байеса, «обратное условие», или правдоподобие – насколько правдоподобны данные В при условии верности априорных данных А. В данном примере это «а насколько часто тогда, когда удавалось доехать до работы за час, выпадал снег?». Это самый важный момент, который учитывает вероятность того, что снегопад все же не помешает доехать до работы за обычное время. Допустим, это случалось редко, в 2% случаев (0,02).
Тогда P(А|В) = 0,02 * 0,9/0,2 = 0,09. Вероятность доехать за час в снегопад составляет всего 9%.
Конечно, вряд ли кто-нибудь, глянув в окно утром снежного понедельника, примется за расчеты по формуле Байеса – скорее всего, просто «на уровне здравого смысла» сразу же придет к такому же выводу, что вероятность уложиться в привычное время маршрута низка и лучше выйти из дома пораньше (ну или заведомо решит опоздать или остаться дома, оправдав это погодой). В том-то и дело, что байесовская формула описывает саму логику «вычислительной машины» разума. Хотя формально людям обычно сложно разобраться в формуле Байеса, принимаемые в повседневной жизни решения вполне сопоставимы с байесовским подходом.
Это вовсе не означает, что все думают одинаково, – напротив, объясняет, почему между людьми зачастую возникают глубокие разногласия: если априорные представления различаются, то одни и те же новые данные могут привести к совершенно разным выводам. И это объясняет, например, почему люди склонны к предвзятости подтверждения. Если человек твердо придерживается какой-то точки зрения, то к противоречащей ей информации будет относиться скептически – то есть придавать ей слишком малый вес в сравнении со своим априорным убеждением. И все это совершенно «по-байесовски», но путем искусственного занижения правдоподобия новых данных.
Формула объясняет и то, почему «простой здравый смысл» иногда подводит. К примеру, медицинский тест точен на 99% (в 99% случаев точно определяет заболевших и в 99% точно определяет не болеющих) и оказался положительным: это вовсе не значит, что вероятность наличия болезни составляет 99%, как может показаться. Если ею болеет 1 человек из 100, то вероятность быть больным при положительном тесте равна только 50% (например, из 1 млн реально болеют 10000, среди которых тест выявит 9900, или 99%; и еще 9900 из 990000 не болеющих, или 1%, получат ложноположительный результат). Повторный же тест в случае положительного первого повысит реальную точность до 99% (прежняя апостериорная вероятность – результат в 50% – стала уже новой априорной).
Если же болезнь более редкая, например 1 случай на 10000 человек, то ее реальная вероятность при положительном результате теста и вовсе менее 1%: поэтому в таких случаях медики обычно не полагаются на один тест и проводят комплексную диагностику. И наоборот, в разгар эпидемии гриппа, когда болеет каждый третий, вероятность наличия болезни при положительном тесте – около 98%. То есть в действительности точность теста зависит от того, насколько распространено заболевание среди населения – например, одного региона, определенной возрастной группы или профессии.
Выведенное в середине XVIII века английским священником и математиком Томасом Байесом и долгое время остававшееся скорее на периферии науки, это уравнение оказалось поразительно востребованным два столетия спустя, а особенно в наше время, – в мире, который становится все более неопределенным. Формула Байеса стала одной из основ теории вероятности – раздела математики, а универсальная байесовская методология для рассуждений в условиях неопределенности объясняет ее широчайшее междисциплинарное применение.
Байесовский подход используется в экономике – например, байесовская векторная авторегрессия (BVAR) позволяет повышать точность макроэкономических прогнозов, в том числе по инфляции (через обновление инфляционных ожиданий), а байесовское оценивание в современных макроэкономических DSGE-моделях применяется в том числе для анализа эффектов монетарной политики. В финансах байесовские принципы служат для оценки рисков, управления портфелем; в психологии – для изучения и моделирования когнитивных процессов; в социологии и политологии – для моделирования динамики общественного мнения; в криминалистике и юриспруденции – для оценки силы доказательств (например, совпадения ДНК) в контексте априорных обстоятельств дела и для формализации логических рассуждений о виновности.
Теорема Байеса широко применяется в науке о данных; она стала краеугольным камнем для машинного обучения, компьютерного зрения и алгоритмов генеративного искусственного интеллекта. Обучающие данные служат для получения апостериорных вероятностей, которые затем используются для прогнозирования будущих данных, а затем, уже в качестве новых априорных, для дальнейшего обучения моделей. Когда ИИ-рентген пытается распознать раковую опухоль на снимке или когда ChatGPT пишет рассказ, они применяют байесовский подход.
Он используется в биологии, биоинформатике и генетике, в астрофизике и квантовой механике, теории информации, нейронауках, медицине и эпидемиологии и вообще везде, где есть априорное знание либо гипотеза, новые данные и необходимость количественно оценить и их, и гипотезу, чтобы получить новые знания, или обновлять убеждения. Решение, принятое в условиях неопределенности, будет правильным в той мере, в какой оно приближается к логике теоремы Байеса, и неправильным в той мере, в какой оно отдаляется от нее.
Идея, которую разработал Байес, является, возможно, самым важным уравнением в истории, рассуждает Том Чиверс: само сознание человека и то, как он воспринимает мир, – байесовские.
«Эконс» публикует отрывок из книги Тома Чиверса «Предсказать все», выпущенной в переводе на русский язык издательством Individuum в январе 2026 г.
***Мы разобрались, как люди в определенных обстоятельствах становятся верными байесианцами: что хотя можно создавать искусственные сценарии, в которых их рассуждения оказываются неверными, и хотя они не очень хорошо справляются с реальными вычислениями по правилу Байеса, наши решения, по-видимому, довольно сильно к нему приближены в более естественных сценариях.
Но можно пойти еще дальше. На самом деле все, что мы воспринимаем в мире, обусловлено теоремой Байеса. Восприятие и само сознание – в довольно прямом смысле – байесовские.
Можно обоснованно возразить, что это почти тавтологическая истина. «Байесовский метод очень хорошо описывает проблемы, с которыми сталкивается мозг», – говорит Анил Сет, нейробиолог из Сассекского университета, занимающийся проблемами сознания. «Мозг сталкивается с неоднозначной сенсорной информацией». Задача мозга – использовать эту информацию, чтобы выяснить ее причину. «Переход от наблюдений к причинам наблюдаемого – это обратное рассуждение, для которого байесовский метод очень хорошо подходит». И поскольку я потратил большую часть книги, чтобы показать, что теорема Байеса лежит в основе всех процессов принятия решений в условиях неопределенности и что любой процесс принятия решений хорош в той мере, в какой он приближается к байесовскому методу, и плох в той мере, в какой не приближается, было бы удивительно, если бы работа нашего мозга не приближалась бы в той или иной степени к Байесу.
Но есть и более серьезное предположение, которое выдвигают некоторые ученые, и заключается оно вот в чем: правило Байеса математически в большой степени описывает работу мозга, основная задача которого – формировать прогнозы о мире, которые он затем комбинирует с информацией, поступающей через органы чувств. То есть мозг обладает некими априорными вероятностями, к которым он добавляет условные вероятности (likelihood) и в результате «выдает» апостериорные вероятности. Происходит этот процесс на самых разных уровнях – от самых базовых, «низкоуровневых» прогнозов о том, какой именно набор нейронов будет работать при движении определенных мышц, до сложных, «высокоуровневых» концептуальных предсказаний вроде «я ожидаю, что сегодня в рабочей столовой будет суп». Эти прогнозы проверяются на соответствие реальности: совпадают ли предсказания с поступающей сенсорной информацией. Если нет, наш мозг должен обновить свою модель мира.
Это противоречит ощущениям от восприятия мира: нам кажется, что мы видим мир через окно. Но мы знаем, что это не так. Мы знаем, что «мы» – это мозг, находящийся внутри костной полости и связанный с внешним миром только мясистыми нитями нервов, которые соединены с органами чувств. Байесовская модель мозга предполагает, что восприятие есть улица с двусторонним движением: информация поступает от органов чувств, но она также поступает и от нашей внутренней модели Вселенной. Наше восприятие – смешение «восходящего» потока с «нисходящим». Эти «потоки» сдерживают друг друга: если «нисходящие» априорные представления сильны, то для того, чтобы их опровергнуть, требуются точные и убедительные данные от органов чувств.
Ученые задавались вопросом о том, как мы воспринимаем мир, на протяжении тысячелетий. Знаменитая аллегория Платона о пещере посвящена как раз восприятию. Узники заперты в пещере и сидят в ней лицом к стене, на которую отбрасывает тени своеобразный кукольный спектакль «в исполнении» огня, горящего позади них. Узники, никогда не видевшие ничего другого, думают, что тени – это и есть реальность, и дают теням имена. По Платону, наше восприятие мира похоже на эту сцену: мы видим не реальность как она есть, а ее тень, опосредованную нашими чувствами.
Однако Платон не был первым, кто обратился к этому вопросу. Философ-досократик Демокрит, живший в V веке до н.э., считал, что вещи в мире постоянно излучают крошечные образы самих себя, eidola, сделанные из атомов, из которых состоит сама вещь. Евклид полагал, что глаза испускают лучи, которые исследуют вещи мира и возвращаются к зрителю с информацией о них. Эти две модели восприятия – лучи, испускаемые глазом, известные как экстрамиссия, или физические формы, испускаемые объектами и воспринимаемые глазом (интромиссия), – доминировали в понимании восприятия, или, по крайней мере, зрительного восприятия, в течение тысячи лет.
Философ X века Абу Али аль-Хасан ибн аль-Хайтам, известный на Западе как Альхазен, первым сформулировал нечто похожее на современную теорию зрительного восприятия. Он утверждал, что свет исходит от светящихся объектов и распространяется по прямым линиям во всех направлениях. Затем этот свет отражается от других объектов, и часть его попадает в глаза зрителя.
Иммануил Кант в XVIII веке говорил, что Вселенная, как она есть на самом деле, непознаваема, и все, что мы знаем, – это мир, воспринимаемый нашими органами чувств: он проводил четкое различие между явлениями (phenomena), нашим восприятием вещей и ноуменами (noumena) – вещами-в-себе. Более того, Кант предвосхитил байесовскую модель мозга: он утверждал, что в нашем мозгу, видимо, есть заранее заложенные концептуальные рамки, с помощью которых мы можем осмыслить мир, иначе данные, поступающие от наших органов чувств, будут бессмысленной мешаниной. Говоря современным языком, у нас должны быть априорные представления. Мы не просто пассивно воспринимаем мир: мы конструируем его или его модель.
Эту идею развил немецкий полимат XIX века Герман фон Гельмгольц, изобретатель офтальмоскопа – маленькой забавной палочки с линзой на конце, с помощью которой оптики рассматривают нашу сетчатку. Но его великое озарение заключалось в том, что мы не можем воспринимать мир таким, какой он есть на самом деле, потому что слишком медленно «работаем».
В эпоху Гельмгольца уже было известно, что нервная система человека имеет электрическую природу и что электричество распространяется чрезвычайно быстро – со скоростью света, – поэтому считалось, что нервные сигналы проходят от органов чувств до мозга практически мгновенно. Учитель Гельмгольца говорил ему, что измерять скорость сигналов не имеет смысла. Но Гельмгольц все равно измерил и обнаружил – к всеобщему удивлению, – что нервные сигналы проходят до обидного медленно: со скоростью около пятидесяти метров в секунду, или 180 километров в час. Он также измерил время, которое требуется человеку, чтобы отреагировать на ощущение, например на прикосновение к руке: для этого нужно было как можно быстрее нажать на кнопку. Гельмгольц обнаружил, что время от ощущения до реакции составляет более десятой доли секунды. Этот факт, по его мнению, доказывал невозможность реальности и мгновенности нашего восприятия мира. Таковое невозможно по той простой причине, что информация, бытующая в мире, не доходит до нас быстро. Если бы восприятие было непосредственным, то мы бы постоянно видели мир с небольшой, но ощутимой задержкой. Если бы я случайно столкнул ручку со стола и попытался ее поймать, я бы целился в пространство в воздухе примерно на пять сантиметров выше того места, где она находится на самом деле.
Гельмгольц утверждал, что наше кажущееся мгновенным и не требующим усилий восприятие мира, должно быть, является иллюзией. Наш мозг производит ряд «бессознательных умозаключений», строя трехмерную модель мира из шумного двухмерного изображения, проецируемого на сетчатку глаза, и столь же шумной и нечеткой информации, поступающей от других органов чувств.
Он приводит пример: представим, некая женщина держит в руке ручку. Ручки касаются три ее пальца. Но каждый палец передает только информацию о контакте с гладким цилиндрическим предметом: прямые сигналы от нервов в ее руке были бы одинаковыми, если бы пальцы касались трех разных ручек. Она воспринимает себя держащей одну ручку, потому что знает, что ее пальцы расположены близко друг к другу. Ее модель мира формирует ее восприятие.
В 1970‑х годах британский психолог Ричард Грегори развил идеи Гельмгольца. Он предположил, что наше восприятие по сути является гипотезой: он провел четкую аналогию с тем, как в научном процессе строятся гипотезы о мире; мы же проверяем такие же гипотезы с помощью органов чувств. Для демонстрации своего предположения он использовал ряд оптических иллюзий. Оптические иллюзии, утверждал он, суть не просто дефекты нашего восприятия: их создает наш мозг, строя тем самым модель мира. Чтобы создать умную иллюзию, мы задействуем «короткие пути», которые использует наш мозг. Это происходит потому, что, по его словам, мозгу приходится выполнять очень много работы. Мир в том виде, в котором он отображается на нашей сетчатке, беспорядочен: начать хотя бы с того, что он перевернут вверх ногами и справа налево (если закрыть глаза и нажать на левый нижний угол одного глаза, то в результате цветное пятно появится в правом верхнем углу зрительного поля). Кроме того, мир искажается из-за вогнутой формы задней части глазного яблока, а также из-за кровеносных сосудов, которые его покрывают. Усугубляет все тот факт, что человеческий глаз просто неудачно «сконструирован»: нервы от сетчатки направлены внутрь, а не наружу, поэтому для того, чтобы дойти до мозга, зрительный нерв должен пройти через сетчатку, из-за чего остается большое слепое пятно. (Забавная игра: закройте левый глаз и сведите оба указательных пальца вместе прямо перед собой, на уровне глаз. Держите левый палец на месте и продолжайте смотреть на него, а правый палец медленно отводите вправо. Когда вы отведете палец примерно на 20 см, верхняя костяшка указательного пальца правой руки исчезнет. Это слепое пятно вашего правого глаза.)
«Задача мозга – не видеть изображение на сетчатке, а соотносить сигналы от сетчатки с объектами внешнего мира», – писал Грегори.
Но здесь возникает проблема. Сигнал из внешнего мира может быть вызван буквально бесконечным количеством вещей. Представьте, что вы находитесь на улице темной ночью и видите на небе одно яркое пятно. Оно маленькое и находится где-то близко: возможно, это светлячок или посадочный прожектор самолета? Или оно огромное, но далекое, может быть, планета Юпитер? Или еще более огромная и далекая звезда Вега? Есть две переменные – размер и расстояние, и мы можем объяснить явление «маленькое яркое световое пятно» бесконечным числом их комбинаций: ближе и меньше, дальше и больше и все, что между ними. «Основная проблема, которую должен решить мозг, заключается в том, что любое конкретное изображение на сетчатке может быть создано бесконечным числом размеров, форм и расстояний до объекта, – писал Грегори, – но обычно мы видим только один стабильный объект».
Грегори предположил, что мозг как раз и занимается тем, что выдвигает гипотезы. Затем он проверяет эти гипотезы, сравнивая их с данными, полученными от органов чувств. Грегори продемонстрировал, что когда две гипотезы одинаково убедительно объясняют доказательства, мозг может между этими гипотезами переключаться. Самый известный пример – «куб Неккера»: если мы с вами похожи, то вы сможете «выбрать», как смотреть на него – сверху и справа или снизу и слева.
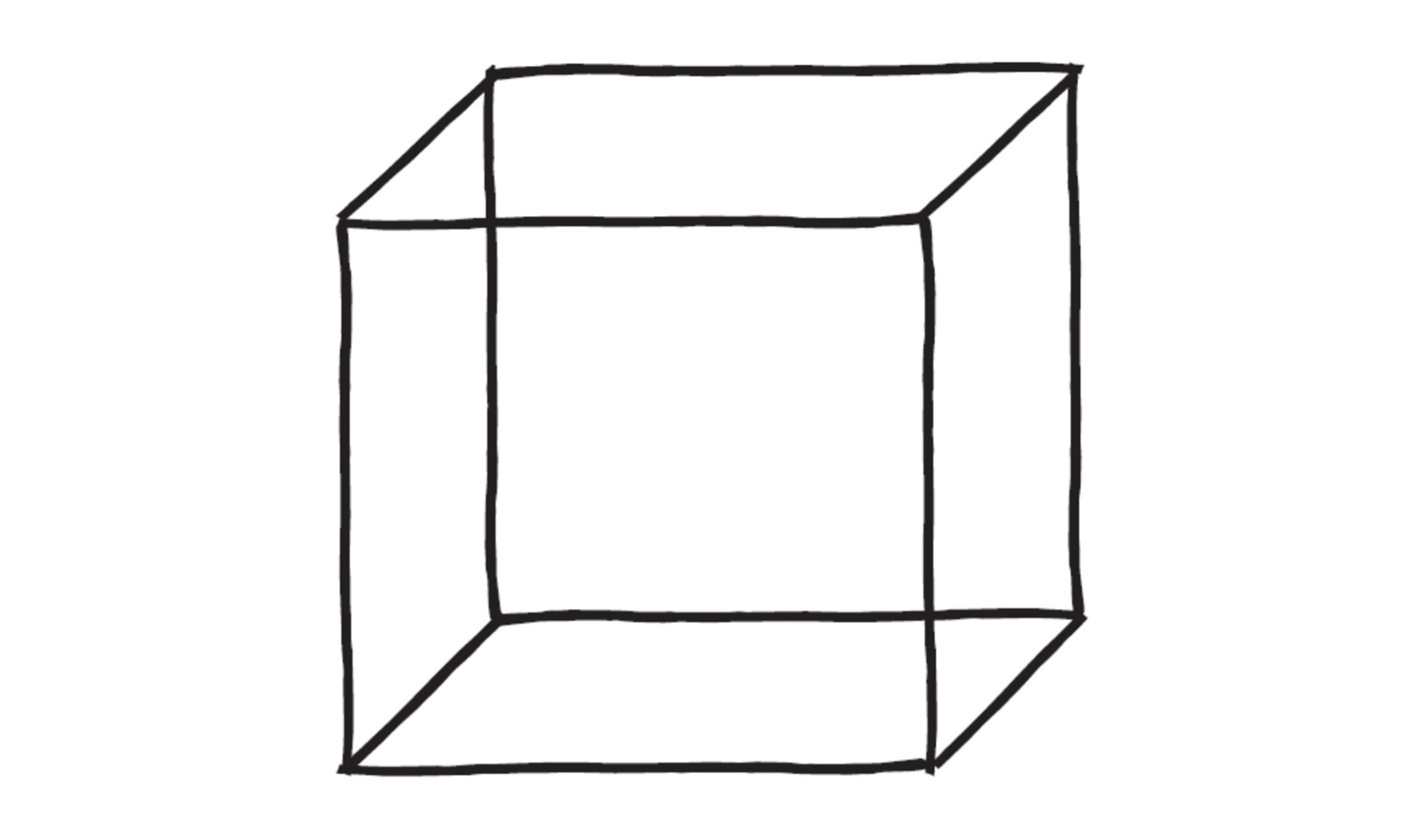
Это, как вы, наверное, уже поняли, и есть байесовская модель восприятия. Гипотезы – это априорные вероятности (представления). Вы ищете новые свидетельства своих ощущений, чтобы подтвердить или опровергнуть их: это и есть ваша правдоподобная вероятность, ваши данные. И вы их комбинируете, чтобы получить апостериорное распределение вероятностей. В случае с кубом Неккера у вас нет веских причин предпочесть одну из двух гипотез (взгляд на куб снизу или сверху), поэтому ваша априорная вероятность делится между ними в соотношении пятьдесят на пятьдесят, а ваши данные одинаково убедительно согласуются с обеими.